Principe de la Radiosité

Dans cette page, vous trouverez la description de la technique de radiosité, mais seuls des algorithmes simples y seront abordés.

Qu'est ce que la radiosité ?

La radiosité est une technique de synthèse d'images réalistes basée sur le calcul des transferts d'énergie entre les surfaces d'une scène. Elle fut inspirée directement par la physique (de la thermodynamique plus précisément). Cette technique a été introduite dans l'informatique graphique grâce aux travaux de chercheurs des Universités d'Hiroshima et de Cornell aux Etats Unis : le tout premier article sur la radiosité a été écrit par Goral en 1984.

Quelles sont les différences entre la radiosité et le lancer de rayons ?

La méthode du lancer de rayons (``Ray tracing'' en anglais), introduite par Whitted, donne des résultats corrects avec des réflexions de type spéculaire (énergie retransmise essentiellement dans la direction de réflexion) mais ne permet pas de prendre en compte des réflexions de nature diffuse (énergie retransmise depuis la surface dans toutes les directions). Pour tenir compte de toutes les contributions lumineuses oubliées, le lancer de rayons ajoute un terme nommé ``intensité ambiante'' qui n'existe pas physiquement.

Bien sûr, dans la réalité, les environnements sont composés de surfaces diffuses tels les murs, les tapis etc... C'est pourquoi le rendu en lancer de rayons peut être décevant pour ce type de surfaces. En réalité, les objets ne sont pas seulement illuminés par des sources de lumière, mais aussi par les lumières émises par les autres surfaces de la scène.
Prenons un exemple concret. Imaginons une scène où une orange serait posée sur une feuille de papier blanc, le tout illuminé par le soleil. Dans la réalité, on pourrait observer sur la feuille blanche un dégradé très léger de couleur orange très clair près de l'endroit où l'orange est posée. Ce type d'effet est très difficile à rendre en lancer de rayons, alors qu'avec la radiosité, il pourra être recréé.

Pour résumer, la technique de radiosité permet de traiter la réflexion diffuse, difficile à mettre en oeuvre en lancer de rayons. En contrepartie, la radiosité classique sera incapable de travailler avec des surfaces spéculaires (des miroirs par exemple), et est généralement plus coûteuse.

Les équations de radiosité :

Précisons d'abord que la radiosité est une mesure physique qui représente un travail énergétique par unité de surface (l'unité est donc watt/m2).

Nous considérons ici que toutes les surfaces sont des surfaces réfléchissantes lambertiennes, qui répartissent la lumière équitablement dans toutes les directions (réflection diffuse). La radiosité n'a pas de dépendance directionnelle.

La physique nous dit que la radiosité Bi partant d'une surface i dépend de la somme des radiosités Bj émises par les surfaces j de la scène, ainsi que l'émittence Ei de la surface i.

En formalisant cela, on obtient l'équation suivante :

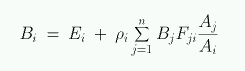
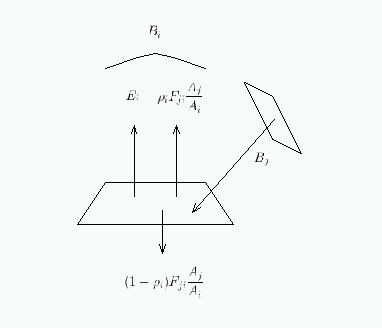Les termes sont les suivants :

• Bi est la radiosité de la surface i.
• Ei est l'émittence de la surface i.
• La surface i est caractérisée par un coefficient surfacique rho(i) de réflectivité qui représente la proportion du flux énergétique que la surface réémet après l'avoir reçue.
• Fji est la fraction d'énergie qui part entièrement de la surface j et qui arrive effectivement sur la surface i. Ce coefficient prend en compte les orientations relatives des surfaces i et j et le fait qu'elles soient éventuellement obstruées par d'autres surfaces. Il s'agit d'un coefficient compris entre 0 et 1 qui est fonction des dispositions géométriques des deux surfaces et du reste de la scène. On le nomme ``facteur de forme''. Il faut savoir que ce facteur de forme est très long et difficile à calculer numériquement (il faut prendre en compte le fait qu'une surface soit éventuellement partiellememnt visible depuis une autre et c'est ce qui prend du temps de calcul.). Les performances des algorithmes de radiosité dépendent beaucoup du nombre de facteurs de forme calculé.
  (Remarque : le calcul des facteurs de forme ne sera pas abordé ici.)
• Ai et Aj représentent l'aire des surfaces i et j.

Remarquons que :

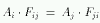
L'équation peut donc être simplifiée en :

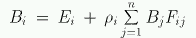
Puis, on peut écrire :

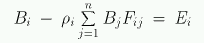
Résolution informatique du problème de radiosité :

Considérons que notre scène 3D est décomposée en plusieurs surfaces rectangulaires, que nous appellerons dorénavant des ``patchs''. On peut donc associer à chacun de ces patchs une équation du type de celle décrite précédemment. En conséquence, le calcul de la radiosité Bi d'un patch i peut être obtenu en résolvant un système linéaire de n équations à n inconnues, qui représente un certain ``équilibre des transferts énergétiques''.

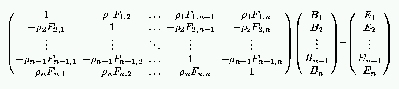
On écrit aussi :

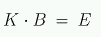
Bien entendu, plus la scène contient de patchs, plus cette résolution est longue et plus l'espace mémoire occupé est important. Il existe heureusement des méthodes qui permettent de converger vers la solution de ce système sans pour autant le résoudre.

Considérons le simple algorithme suivant :

1. On calcule donc tous les facteurs de forme pour chaque couple de patchs (c'est généralement ce qui prend le plus de temps).
2. Pour quelques longueurs d'ondes du spectre visible (pour simplifier, on ne considère que les couleurs rouge, vert et bleu), on construit la matrice décrite précédemment.
3. Pour chaque longueur d'onde on résoud le système, on obtient donc pour chaque patch i la radiosité Bi associée au rouge, ainsi que celle au vert et au bleu.
4. On calcule ensuite la radiosité aux quatre sommets de chaque patch associée à une longueur d'onde (pour nous, seulement les couleurs rouge, vert, puis bleu). Ceci peut être réalisé par moyennage des radiosités des patchs communs à chaque sommet.

Visualisation :

Ces calculs étant terminés, il est maintenant possible d'afficher le résultat en dessinant chaque patch, en réalisant une interpolation des couleurs calculées aux quatre sommets. La technique généralement utilisée est l'interpolation bilinéaire de Gouraud.

Propriété d'indépendance de la position de l'observateur :

Les calculs de radiosité, contrairement à ceux du lancer de rayons, sont indépendants de la position de l'observateur (c'est à dire qu'à aucun moment, dans les calculs, la notion d'observateur n'intervient).
En conséquence, on peut calculer une scène en lui appliquant un algorithme de radiosité une fois pour toutes. Et, une fois ceci réalisé, on peut positionner un observateur à n'importe quel endroit et visualiser en temps réel le résultat si la taille de la scène le permet.

Applications :

Le fait que la radiosité soit une solution indépendante de la position de l'observateur est un avantage considérable par rapport à la technique du lancer de rayons. En particulier pour la réalité virtuelle, la radiosité offre des possibilités de réaliser des déplacements interactifs dans des scènes 3D visualisées de façon réaliste.

De plus, la radiosité se prête bien aux calculs d'images de bâtiments, d'architecture et d'urbanisme. On peut, par exemple, imaginer, simuler, tester et adapter le positionnement de sources lumineuses avant de le réaliser physiquement.